Log mean temperature difference
The log mean temperature difference (also known by its acronym LMTD) is used to determine the temperature driving force for heat transfer in flow systems, most notably in heat exchangers. The LMTD is a logarithmic average of the temperature difference between the hot and cold streams at each end of the exchanger. The larger the LMTD, the more heat is transferred. The use of the LMTD arises straightforwardly from the analysis of a heat exchanger with constant flow rate and fluid thermal properties.
Contents |
Definition
We assume that a generic heat exchanger has two ends (which we call "A" and "B") at which the hot and cold streams enter or exit on either side; then, the LMTD is defined by the logarithmic mean as follows:
where ΔTA is the temperature difference between the two streams at end A, and ΔTB is the temperature difference between the two streams at end B.
This equation is valid both for parallel flow, where the streams enter from the same end, and for counter-current flow, where they enter from different ends.
A third type of flow is cross-flow, in which one system, usually the heat sink, has the same nominal temperature at all points on the heat transfer surface. This follows similar mathematics, in its dependence on the LMTD, except that a correction factor F often needs to be included in the heat transfer relationship.
There are times when the four temperatures used to calculate the LMTD are not available, and the NTU method may then be preferable.
Application
Once calculated, the LMTD is usually applied to calculate the heat transfer in an exchanger according to the simple equation:
Where Q is the exchanged heat duty (in watts), U is the heat transfer coefficient (in watts per kelvin per square meter) and A is the exchange area. Note that estimating the heat transfer coefficient may be quite complicated.
Derivation
Assume heat transfer is occurring in a heat exchanger along an axis z, from generic coordinate A to B, between two fluids, identified as 1 and 2, whose temperatures along z are T1(z) and T2(z).
The temperature differences are ΔT(A) at point A and ΔT(B) at point B, having defined ΔT(z)=T2(z)-T1(z).
Note that the direction of fluid flow does not need to be considered; it is also unimportant which stream is the hot and which is the cold one, as a change of role will be represented by negative numbers. Since LMTD is the average temperature difference of the two streams between A and B, it is defined by the following formula:
- Assumption
- The rate of change of the temperature of the two fluids is proportional to the temperature difference between them:
This gives:
where K=ka+kb.
We can now express dz as a function of ΔT:
Substituting this expression back into our formula for LMTD, we can remove dz from it:
K is constant and can be simplified. Integration is at this point trivial, and finally gives:
Assumptions and Limitations
- It has been assumed that the rate of change for the temperature of both fluids is proportional to the temperature difference; this assumption is valid for fluids with a constant specific heat, which is a good description of fluids changing temperature over a relatively small range. However, if the specific heat changes, the LMTD approach will no longer be accurate.
- A particular case where the LMTD is not applicable are condensers and reboilers, where the latent heat associated to phase change makes the hypothesis invalid.
- It has also been assumed that the heat transfer coefficient (U) is constant, and not a function of temperature. If this is not the case, the LMTD approach will again be less valid
- The LMTD is a steady-state concept, and cannot be used in dynamic analyses. In particular, if the LMTD were to be applied on a transient in which, for a brief time, the temperature differential had different signs on the two sides of the exchanger, the argument to the logarithm function would be negative, which is not allowable.
References
- Kay J M & Nedderman R M (1985) Fluid Mechanics and Transfer Processes, Cambridge University Press
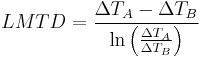
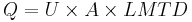
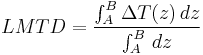
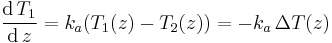
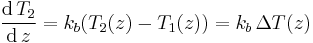
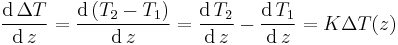
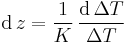
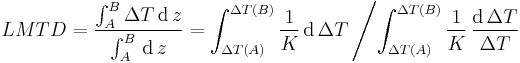
![LMTD = \int^{\Delta T(B)}_{\Delta T(A)}\mathrm{d}\,\Delta T \left/ \int^{\Delta T(B)}_{\Delta T(A)} \frac{\mathrm{d}\,\Delta T}{\Delta T} \right.
=[\Delta T]^{\Delta T(B)}_{\Delta T(A)} \left/ [\ln{\Delta T}]^{\Delta T(B)}_{\Delta T(A)} \right.
=\frac{\Delta T(B)-\Delta T(A)}{\ln [ \Delta T(B) / \Delta T(A) ] }](/2012-wikipedia_en_all_nopic_01_2012/I/6275ab3d8c02c611c053c221d1eef22f.png)